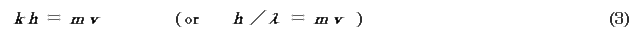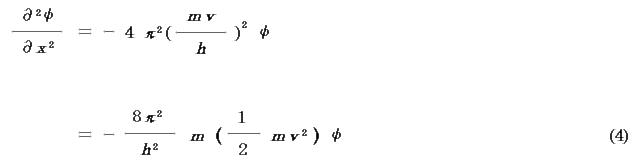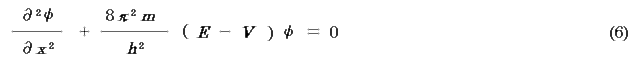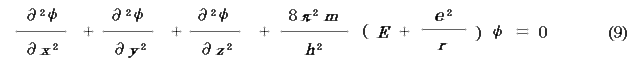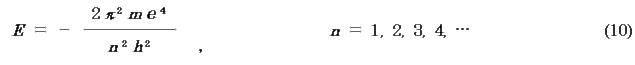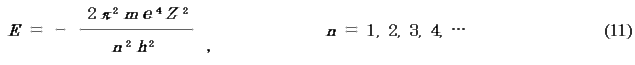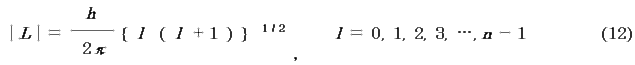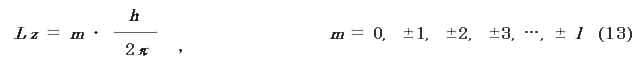【概説】波動方程式と量子論
まとめ: ecosci.jp 本間善夫
1.シュレディンガーの波動方程式
シュレディンガーは電子にも波の一面があると考え,物質波に対する波動方程式を立てた.
波の状態を示す値をψ,振幅をA として,正弦関数で波を表すと,
ここで,k は波数(波長をλ とすると,k = 1/λ),ν は振動数である.これを2回偏微分(∂ は偏微分記号)すると,
これは波動を示す一般的な微分方程式である.
速度v で運動する質量m の粒子の運動量には,
の関係がある(h は Planck 定数).よって(2)式は,
粒子の運動エネルギーT ,ポテンシャルエネルギーV ,全エネルギー(粒子の量子化された許容エネルギー)E の間には次の関係がある.
よって(4)式は,
3次元について考えれば,次のようになる.
これが定常状態(t を考えない)の物質波を示すシュレディンガーの波動方程式であり,ψ を波動関数という.粒子系のポテンシャルV を式に入れて解けば波動関数と全エネルギーを求めることができる.しかし,この方程式を解くのは容易ではない.
また,波動方程式を水素原子のような実際の系に適用してみると,エネルギーE が種々の互いに整数で関係づけられたある値をとらない限り解けないことがわかる.つまり,量子化されたエネルギーや量子数は シュレディンガー理論から必然的な結果として得られる(Bohr の理論では仮定が必要になる).
● ψ とは? : ψ 自身には物理的な意味はないが,│ψ │2 には重要な物理的解釈が与えられている.それは,場所によって粒子を見出す確立がどう変化するかを数学的に表したものである.つまり,量子力学には Bohr のような明確な軌道は現れてこないわけである.
2.水素原子の波動方程式
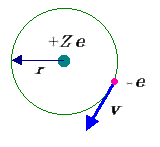
図1 Bohr の原子モデル(電子数=1).Z は原子核上の単位電荷[e ]の数(陽子数と考えてよい)であり,水素ではZ = 1.
Bohr 原子の考えより,電子の軌道が力学的に安定なことから,電子−原子核間のクーロン力(点電荷間の静電気力)が,円運動による遠心力とつり合っていなければならないので,一般に,
水素原子ではポテンシャルエネルギー(クーロンエネルギー)V は,
であるから(e は電気素量,r は中心からの距離),シュレディンガーの波動方程式は,
この方程式は,直交座標では解けないので,極座標に変換する.解法を省略して,以下に結論を示す.電子の軌道(正確には orbital )は以下の4つの量子数によって決まる.
(i) 距離r に関する式を解くことにより,E を得る.
※核電荷Z の任意の1電子原子では一般に,
Bohr は仮定を設けて同じ結果を得てn を導入したが,波動方程式では微分方程式の解が存在するのに必要な数値として極めて自然にn が導入される.n を主量子数という.
(ii) 電子の全角運動量L は,次式で与えられる.
l も自然に導入される整数で,方位量子数(角運動量子数)という.
(iii) ある軸方向の角運動量Lz は,
で与えられ,m を磁気量子数という.
電子の波動関数および全エネルギーは,n ,l ,m によって定められる.なお,l = 0,1,2,3,… に応じて,s,p,d,f,… 軌道という呼び方がなされる.
(iv) 電子自体も回転の角運動量をもっており,それをスピン角運動量という.磁場の中では磁場の方向をとるものと反対の方向をとるものがある.それを規定するのがスピン量子数s であり,+1/2 か −1/2 である.
《量子論の入門書》
- 大岩正芳,「初等量子化学(第2版)」,化学同人
- 並木美喜雄,「量子力学入門」,岩波新書(1992)
- B.H.メイアン 著,塩見賢吾・吉野喩吉・東慎之介 訳,「メイアン 大学の化学 第2版〔II〕」,廣川書店(1972)
- J.C.ポーキングホーン 著,宮崎忠 訳,「量子力学の考え方」,講談社ブルーバックス(1987)
- 原康夫,「量子の不思議」,中公新書(1985)
- 小暮陽三,「絵でわかる量子力学」,日本実業出版社(1990)
- 大木幸介,「量子生物学」,講談社ブルーバックス(1969)
- 大木幸介,「こころの量子論」,日経サイエンス(1984)
「生活環境化学の部屋」に戻る | 計算化学演習メニュー